【column】2次関数
放物線
y=xの2次式で表される関数を2次関数といい、y=ax²+bx+cを「放物線の方程式」といいます。
そのグラフはこのようになります。

ところで放物線ってご存知でしょうか?

そうです。ボールを投げた時のボールの軌道のことです。
なぜ放物線のグラフというのでしょうか?
結論を言うと、
a,b,cを実数の定数として、ものを投げた時のその軌道は
y=ax²+bx+c
で表される
からです。
今からそれを証明しますが、サインやコサインなど三角比の知識&物理的な知識が必要なので軽く流してもらって結構ですが、流し見程度はしていただきたいです。

ただ単にものを投げた軌道が数学と繋がってるんです。しかもただの2次式で表されるんです。
数学って凄くないですか?美しくないですか?
実はこれだけではなく、世界の、宇宙のあらゆるものを数学で驚くほど綺麗に説明できたりするんです。
数学って非常に「美しい」んです。
この感覚をもっといろんな人に知って欲しいな…
1次関数の最大値・最小値【数Ⅰ】
絶対値のついた1次関数のグラフ
y=|2x/3 - 2|のグラフをかけ。
絶対値記号の中が正か負かで場合分けします。
すると、
[1] x<3のとき y= -2x/3 + 2
[2] x≧3のとき y= 2x/3 - 2
となります。

上の図だと
xが3より小さい時→赤のグラフ
xが3以上の時→青のグラフ
になります。
よって求めるグラフは下図の実線部分。

ちなみに…
y=|f(x)|などのように絶対値を含んだ関数のグラフは、場合分けの分かれ目であるxで必ずグラフが繋がっていることが知られています。
なので上のような問題は、場合分けの分かれ目のxを少なくとも1つの場合に含める必要があります。
(「少なくとも1つ」なので「x≦3」と「x≧3」で場合分けしても間違いではないです。)
1次関数の最大・最小

絶対値があるのでこの場合も場合分けをします。
絶対値が来たら場合分けです。

図は

ここで疑問を持った方はいませんか?
「最大値なし」ってどういうこと?
見た感じy=2が1番大きそうですが…
x=4は定義域に含まれていません。
xが3.9,3.99,3.999,…と4に近づいていくと、それにつれてyも1.9,1.99,1.999,…と2に近づいていきます。
しかし、これは無限に続いていきますが、x=4を絶対に取らないので決してyも2になることはありません。

無限に続いてしまうので「最大値はコレ!」と決められないので「最大値なし」と答えるしかないんです。
それでは今日はここまで。さようなら。
定数関数・1次関数【数Ⅰ】
定数関数・1次関数
a, cを定数として、関数y=ax+cのグラフは直線になります。これを直線y=ax+cといい、y=ax+cをこの直線の方程式といいます。
このように、yがxの1次式で表される関数を1次関数といいます。
ここでa=0のとき、y=cとなりxの値に関係なくyの値は常に一定となります。このy=cのようにy=(定数)となる関数を定数関数といいます。
まとめると、関数y=ax+cのグラフは
①a>0のとき
傾きがa(右上がり)、y切片(y軸との交点)がcの直線
②a<0のとき
傾きがa(右下がり)、y切片がcの直線
③a=0のとき
傾きが0、y切片がc、x軸に並行な直線
となります。

関数【数Ⅰ】
関数
定数:値が固定されて変化しない数のこと。ただしその値が具体的な数値として特定されていなくてもよい(つまり文字でもOK)。
変数:値が変化する数のこと。未知または定まっていない数を表す。
2つの変数x, yがあり、
xの値を決める→yの値がただ1つに定まる
とき、yはxの関数であるといいます。
また、yがxの関数であることを y=f (x)やy=g(x), y=h(x)のように表します。
これが超超超超超重要なのでかみ砕きます。
関数はよく自動販売機に例えられます。
自動販売機はボタンを押すとただ1つ決まった商品が出てきます。
関数y=f (x) も、
xの値を決める(ボタンを押す)とただ1つyの値が決まり(決まった商品が出てき)ます。
例えば
y=x+2
において、
x = 5 と決めると、ただ1つyの値は y = 7 に決まります。
なのでこの式においてyはxの関数です。
また、y = 3 と決めると、ただ1つxの値は x = 1 に定まるので
xはyの関数でもあります。→逆関数の存在(数Ⅲ)
y=x2
において、yはxの関数です。
ですが、y= 4 と決めてもxの値は x = ±2となり、ただ1つに決まりません。
なのでxはyの関数ではありません。
したがって、
yがxの関数であってもxはyの関数であるとは限らない
ということになります。
数学的な細かい考え方や数Ⅲで効いてくるのでぜひ知っておいてください。
値
関数 y=f(x) において、x=a のときのyの値を f(a) と書き、f(a) を f(x) の x=a における値といいます。
定義域・値域
以下、関数 y=f(x) を考えます。
定義域:xの値が取りうる範囲(xの変域)のこと。ex) y=√x の定義域は x≧0
値域:xが定義域全体を動くときのyの変域のこと。
定義域は(a≦x≦b)のように表すことが多いです。
また定義域について特に断りがないとき、xの定義域は実数全体であることが多いです。
座標
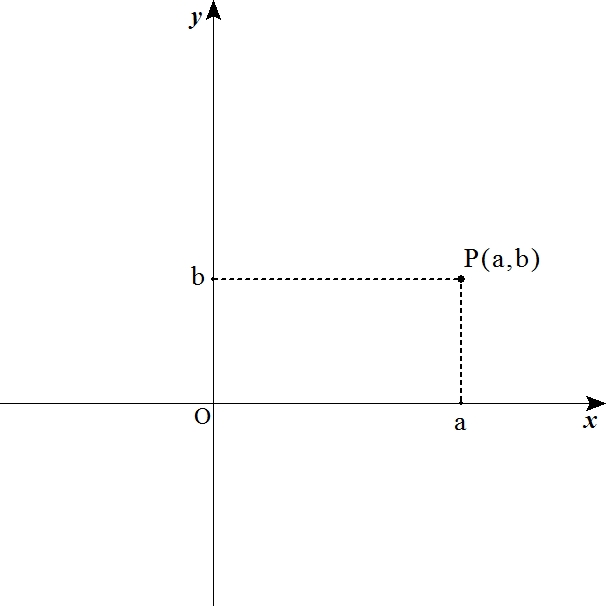
図のように平面上に座標軸(x軸・y軸)を定めると、その平面上のどんな点Pも図のような実数aとbの組で表されます。
この組(a, b)を点Pの座標といい、座標が(a, b)である点PをP(a, b) と表します。
座標軸が定められた平面を座標平面といいます。
また、座標平面で
・x>0かつy>0の領域を第1象限
・x<0かつy>0の領域を第2象限
・x<0かつy<0の領域を第3象限
・x>0かつy<0の領域を第4象限
といいます。
ただし、x軸とy軸はどの象限にも含まれません。
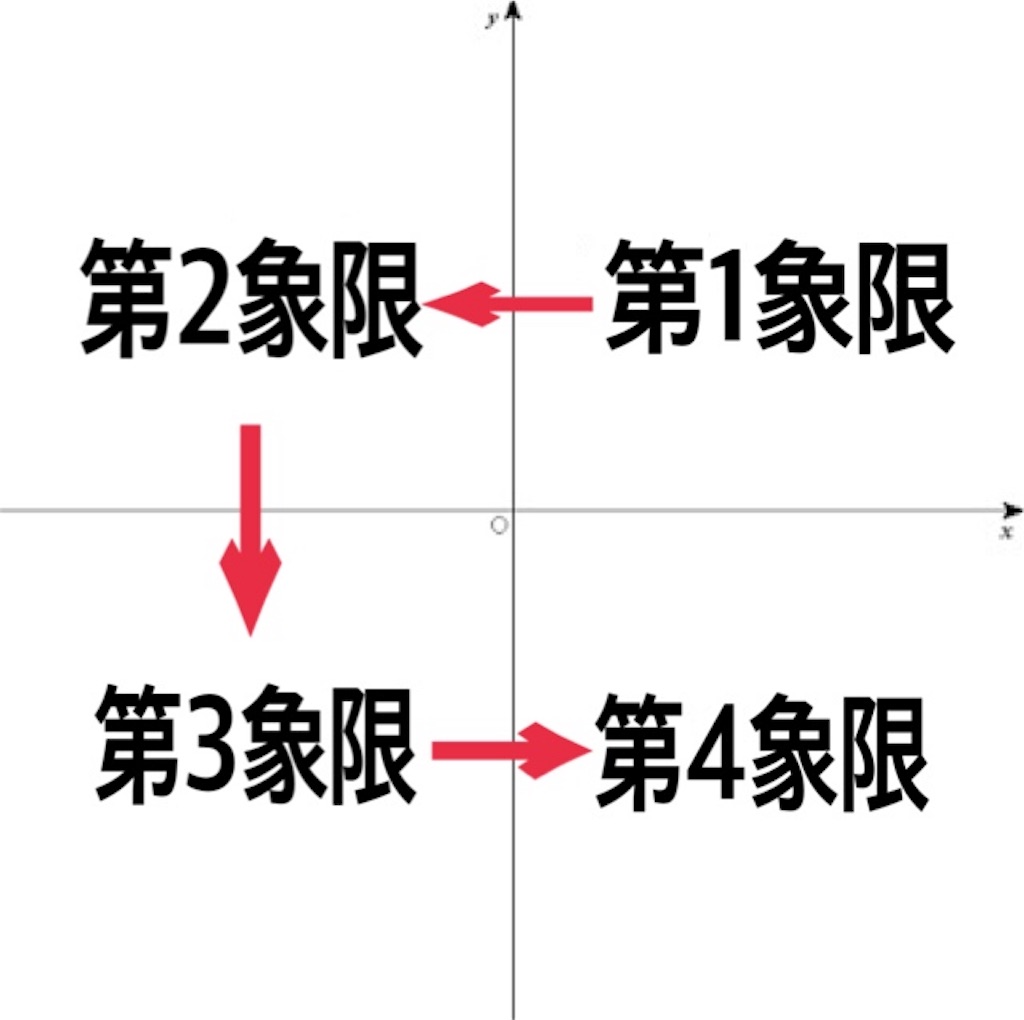
右上から反時計回りですね♪
命題と証明【数Ⅰ】
逆・対偶・裏

1項目目はそのように言う、と決まってるので理屈云々じゃなく覚えましょう。
仮定と結論をひっくり返したのが「逆」です。
否定したのが「裏」です。
逆の裏が「対偶」です。
問題は2項目目。
めちゃくちゃ大事です。
なぜこうなるのでしょう?
色塗りで確かめます。

よって
命題p⇒qを証明するとき、その対偶命題を証明しても良い。
背理法
もう一つ別の証明方法を。
ある命題Xが成り立たないと仮定して矛盾を導くことで、Xが成り立つと結論付ける証明方法を背理法といいます。
背理法の手順
簡単にまとめます。
1.証明したい命題が成り立たないと仮定
2.矛盾を導く
3.命題は正しいと結論
例題で理解しましょう。
有名な問題です。

(※互いに素:1以外に公約数をもたないこと。詳しくは数Aで学習)
結構背理法を使う時があるので使えるようにしましょう。
それでは今日はこの辺で。さようなら。
必要条件・十分条件【数Ⅰ】
必要条件・十分条件
結論からいきましょう。このようにいいます。

必要条件⇒十分条件 です。
よく分からないと思いますが、例題を通して見ていきましょう。

両方向の矢印について考えます。

一言で言いましょう。
矢印の向きで考えるのは分かりづらい!
そして間違えやすいです。
なのでこれで覚えましょう。

遠回りっぽいですが、こっちのが圧倒的に楽です。
例題でやってみましょう。

A∩Bのとき必ずaとbは偶数だと分かったのでA∩B={1, 2}の集合が内側に入ってます。
反例があるので「a, bともに〜」の集合が内側に入ることはありません。
という訳でこのような図になります。
あとはゴロの通り!
どうです?
見た目で十分条件か必要条件か判断しやすくないですか?
このブログを見た方は是非この考え方を忘れないでほしいです。
それでは今日はこの辺で。さようなら。
条件の合成・否定とド・モルガンの法則【数Ⅰ】
条件の合成と否定
今回は短めにいきましょう。
条件p, qを満たすもの全体の集合をP, Qとします。
このとき、条件
・pでない
・pかつq
・pまたはq
はそれぞれP, Qを用いて表すと

となります。
よって、ド・モルガンの法則より

まとめると

それでは今日はこの辺で。さようなら。