集合(2)【数Ⅰ】

集合の要素の表し方

前回書き忘れたので集合の要素の表し方について。

例えば1~9までの奇数全体の集合をAとすると、Aの要素は

1,3,5,7,9

です。これを

A={1,3,5,7,9}

と表します。

また、このAの要素である数xすべてについて

・xは奇数

・xは1以上9以下

ということが成り立ちます。

これを

A={ x｜1≦x≦9, xは奇数 }

と表します。

また、奇数はある整数nを用いると

2n-1と表せます(試しに適当な整数をnに入れてみて確認してください。奇数になります)。

1以上9以下の奇数なので

1≦2n-1≦9

各辺に1を足して

2≦2n≦10

各辺を2で割って

1≦n≦5

ということでnの範囲が出たので、集合Aは

A={ 2n-1｜1≦n≦5, nは整数 }

とも表せます。

以上要素の表し方3パターンです。

{ }の中は

・{要素,要素,要素,要素,…}

・{要素の代表(文字使用)｜文字の条件}

で表します。

それでは今日はこの辺で。さようなら。

集合(1)【数Ⅰ】

用語編

今までのは中学の延長的なところがありましたが、そろそろ中学数学では全く触れない概念が出てきます。

まず用語からいきますか。

集合:範囲がはっきりしたものの集まり

要素(または元):集合を構成するもの一つ一つのこと

有限集合:有限個の要素からなる集合

無限集合:無限に多くの要素からなる集合

xがある集合Aの要素である時 x∈A と書きます。

yが集合Aの要素でないとき y∉A と書きます。

また、「x∈A ならば x∈B」が成り立つ時、AはBの部分集合であるといい、A⊂B と書きます。

空集合:要素を1つももたない集合。∅で表します。任意の集合Aについて ∅⊂A 。

共通部分:集合Aと集合B両方に属する要素全体の集合。A∩B で表します。(3つ以上の集合でも同様)

和集合:集合Aと集合Bの少なくとも1つに属する要素全体の集合。A∪B で表ししまします。

全体集合:集合を考える時、ふつう最初に1つの集合Uを決めて、その要素だけを考える。この最初の集合Uのことを全体集合という。

補集合:全体集合のなかである集合に属さない集合のこと。Ā で表します。

何言ってるかわかりませんよね。

今からめちゃくちゃ噛み砕きます。

めっちゃ噛み砕きます

話は変わりますが、皆さんアイドルは好きですか？

集合を説明するために、アイドルの力を借ります。

以下は下の図(ベン図といいます)と一緒にご覧下さい。

全体集合はアイドルです。

AKB48というグループがあります。これも1つの集合です。

新潟を拠点とするNGT48というグループもあります。

柏木由紀はAKBのメンバーなので

柏木由紀∈AKB 

(柏木由紀はAKBという集合の要素)です。

また、柏木由紀はNGTも兼任しているため

柏木由紀∈NGT

です。このとき、

柏木由紀は両方に所属しているため

柏木由紀∈AKB∩NGT

です。

AKBの中に「ノースリーブス」というユニットがあります。

これはAKBのメンバーで構成されているので

ノースリーブスはAKBの部分集合

つまり

ノースリーブス⊂AKB

です。

AKBとNGTのメンバー全員を合わせて「A&N48」と呼ぶことにすると(実際はそう呼びませんが)

AKB∪NGT=A&N48

となります。

また、ももクロのメンバーかつAKBのメンバーである、という方はいないので

ももクロ∩AKB=∅

です。

また、松潤もアイドルですが、ももクロのメンバーではありません。なので

も成り立ちます。

ここで注意したいのが、それぞれの記号は集合どうしをつなぐのか、集合と要素をつなぐのかをしっかり理解しなければいけない、ということです。

簡単にまとめると

・(要素) ∈(集合)

・(集合)∩(集合)

・(集合)∪(集合)

・(集合)⊂(集合)

となります。

アイドルに疎い方には逆に分かりづらい例えだったかもしれません。

ちょっとネットを調べていただければ僕が言わんとしていることが伝わると思うのでアイドルに疎い方は少しでいいので調べてみてください。

別にアイドルじゃなくても、野菜でもなんでもいいので、何わかりやすいものに例えるのがわかりやすいです。皆さんもやってみてはどうでしょう？

それでは今日はこの辺で。さようなら。

絶対値を含む不等式【数Ⅰ】

|x|=c (c>0)の解について考えてみましょう。

c>0という条件は絶対値は必ず正 ということから来てます。

このときxの符号は+かもしれないし、-かもしれません。

わからないのでどっちも考えてみます。

もしxの符号が+またはx=0のとき、数学っぽく言うとx≧0のとき、絶対値記号はそのまま外せます。よって

x=c

です。(x=0のときも| |をただ外すだけでいいのでx>0のときと一緒にまとめました)

xの符号が-、すなわちx<0のとき、絶対値記号は-を| |の中身にかけて外します(忘れた方は過去ブログhttp://mathematics-for-universe.hatenablog.com/entry/2017/03/25/093350をcheck！)。なので

-x=c

すなわち

x=-c

です。

まとめると

cが正の時

|x|=c の解は x=±c

となります。

絶対値を含む不等式

一般に、次のことが言えます。

c>0のとき

|x|<c の解は -c<x<c

|x|>c の解は x<-c, c<x

これは覚えなくてOKです。

覚えてればはやいですがあまり勧めません。

なぜならこんな間違え方をしてしまうからです。

[結論は偶然正解になりましたが、解答記述としては不正解です。]

何が違うか分かります？

上のように簡単に絶対値が外せるのは右辺が正のときだけです。

ですがこの場合、右辺が3xです。xが-100とかになって右辺が負になる可能性もありますよね。

だから簡易的に外すやり方でやると間違いなんです。

だから、この簡易的に外す方法に頼るより、原理原則に立ち返って絶対値を外した方が安全で確実です。

じゃあその「原理原則」とはなんでしょう。

それは

⑴絶対値記号の中身が正のときと負のときとで場合分け。

⑵正のときはそのまま絶対値を外す。

⑶負のときは中身にマイナスをかけて外す。

⑷⑵と⑶の結果を「または」でつなぐ。(つまり両方答えにする)

 です。これは不等式でも一緒です。

では正答を見てみましょう。

[1]ではxの中身が正または0のときのことだけを考えます。

つまり、[1]ではx-4≧0という条件を設けます。

x-4≧0のときx≧4なので、[1]の中での解は最低でもxが4以上である必要があります。

絶対値を外して解いていくと、x<-2となってx≧4をみたしません。

なので「[1]で決めた条件の下では解はない」と結論します。

同じように[2]ではx-4が負、すなわちx<4という条件を設定します。

解いていくとx<1という答えが出てきます。

このとき、x<4とあらかじめ設定してあるので、これも満たすように答えなければいけません。

なので[2]での解はx<1となります。

そして、求める答えは「[1]または[2]」なので、両方の答えを解とします。

今回はたまたま[1]が解なしだったので、答えは[2]の解になります。

どうでしょう。

原理原則に立ち返れば、たとえそれが簡易的に絶対値記号を外せる問題だとしても、そうでないとしても、絶対値記号を外せます。

だからこの絶対値を含む不等式は、原理原則に忠実に解いてください。

今回はここまで。

それではまた次回お会いしましょう。さようなら。

１次不等式と連立不等式【数Ⅰ】

１次不等式の解法

一言でいいます。

１次方程式と同じです。（※ただし不等号の向きに注意！！）

まあ、練習問題を通してみていきましょう。

［訂正］「不等号」の「号」の字を間違えてしまいました...すみません。

１次不等式と同じように左辺に文字を含んだ項を、右辺に定数項を移項します（もちろん左辺と右辺は逆でもＯＫ）。

そして１次不等式と同じように、左辺がxだけになるように式変形して終了です。

連立不等式

２以上の不等式が連立された連立不等式は、数直線を駆使します。

これは一例ですが、数直線では不等式をこのように表すことが多いです。

では、実際に問題をやってみましょう。

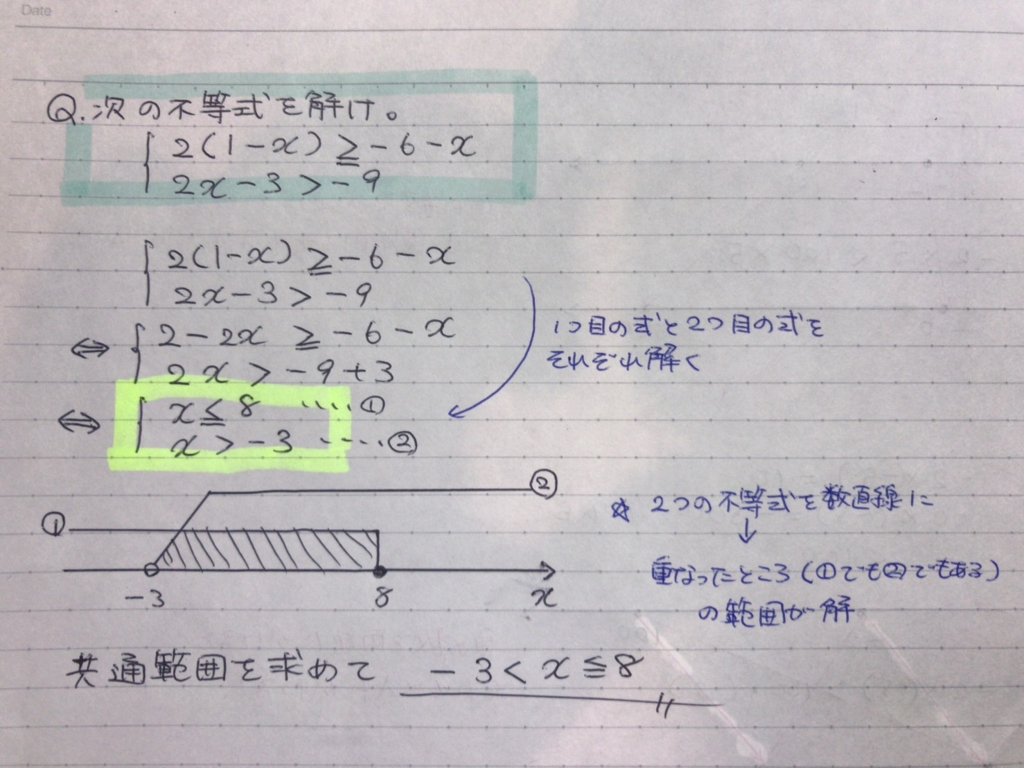
これは２本の１次不等式を連立させた連立不等式です。

まず、この２本の不等式をそれぞれ解きます。

そうすると、黄色の四角の中のようになります。

ここで気を付けるのが｛ は「～かつ・・・」という意味だということです。（後で集合の範囲で詳しくやります）

「～かつ・・・」なので、①でもあり②でもあるｘの範囲がこの連立不等式の解です。

①でもあり②でもある範囲は、２つの不等式を数直線にかいたときに重なる部分（範囲）です。ちなみに重なる部分がないとき、「解なし」といいます。（解がない、という答えです。「解」と「答え」は違うんですねえ）

もう１問。

前回のブログの言葉を借りますね。

この問題は自分で「和訳」してみましょう。

この問題のポイントは「分けて考える」ことです。

今回はここまで。

それではまた次回お会いしましょう。さようなら。

１次不等式の性質【数Ⅰ】

お久しぶりです。

最近忙しく、なかなか更新できませんでした。

新入生はそろそろ高校の勉強が本格的にスタートした頃でしょうか。

新年度、勉強頑張りましょう。

それでは不等式に入ります。

１次不等式の性質

１次不等式において次が成り立ちます。

教科書や参考書にはこんな感じにまとめられています。

②とか訳わからないですよね。

ということで、ちょっと書き直してみます。

どこが変わったかわかりますか？

言っていることは同じなのですが、直感的にこっちのほうがピンとくると思うのでぜひこっちで覚えましょう。

では、ひとつひとつ見ていきましょう。

最初の推移律はその通りです。

当たり前といえば当たり前です。

①ですが、簡単に言うと「移項できる」ってことです。

もうちょっと踏み込むと「足し算・引き算は等号と同じように計算してもいいよ」ということです。

面倒なのは②です。

-2と100を例にとって考えてみましょう。

こんな感じで、不等式の

両辺に正の数をかけたら大小関係はそのまま、

負の数をかけたら大小が入れ替わる（不等号の向きが逆になる）

ということを②で言っています。

ここ、計算ミス多発するので注意しましょう！

少し話題はそれますが、

こういう性質や公式などが出てきたときは先生や参考書に解説されますよね。

僕はこれを「日本語訳」だと思っています。

僕らはたいてい、英語を読むときには和訳をします。（英文のまま頭にイメージできるのがベストですし、長文読解ではその力も求められますが...）

ハリーポッターだって翻訳されて出版されます。

それは、たいていの人は日本語に直した方が理解できるからです。

ですが、物理や数学で「公式」という「異なる言語」が出てくると、なぜかほとんどの人は「異なる言語」のまま、ただ覚えようとします。「エーニジョウプラスビーニジョウイコールシーニジョウ、エーニジョウプラスビーニジョウイコールシーニジョウ、エーニジョウプラスビーニジョウイコールシーニジョウ、、、、、」といった具合に。

数式は言葉です。

もう一度言います。

数式は「理科と数学の世界で使われる外国語」です。

いったん「和訳」をして、じっくり理解してみませんか？

それだけで数学力は変わります。

「エーニジョウプラスビーニジョウイコールシーニジョウ」と覚えるのではなく、「直角三角形の斜辺以外の長さを２乗して足したら斜辺の長さの２乗になる」と覚えるんで

す。

それだけで世界が変わります。

今回はここまで。

それではまた次回お会いしましょう。さようなら。

２重根号【数Ⅰ】

２重根号

のように、ルートの中にルートがあるときがあります。

（これは３重、４重.....と無限に増やせます）

このように根号が２重になっている場合、

根号が２重でない簡単な形にできるときがあります。

必ずできるわけではありません。

２重根号について、次のことが成り立ちます。

以下、証明です。

パソコンで作るのが面倒だったので申し訳ありませんが手書きです←オイ！

この公式も暗記しますか？

答えはＮＯです。

絶対忘れます。

しかもこんなの公式忘れたらおしまいです。（見た目がやばいから 笑）

だから、導出の仕方を理解しましょう！

忘れても公式を出せるようにしましょう！

（公式はすぐ忘れますが、不思議なことに導出の仕方はしっかり理解していれば忘れないものです）

簡単に大雑把に解説します。

 [訂正]√の中が正になる→√〇が必ず正になる

(√a+√b)²を展開して両辺にさらにルートをつける。これだけです。

（左辺と右辺がイコールなんだから、両辺の正の平方根もイコールですよね♪）

見た目の複雑さほど導出は難しくありません。

せっかくなので問題をやってみましょう。

公式にただ突っ込むだけの問題はやりませんよ！

ちょっとひとひねり必要な問題です。

参考書にはたくさん類題があるのでやってみましょう。

今回はここまで。

それではまた次回お会いしましょう。さようなら。

有理化【数Ⅰ】

有理化

有理化：分母に根号が含まれない形に変形することを、分母を有理化するといいます

有理化では、２次式の展開の公式（展開公式【数Ⅰ】 - 宇宙を歩く高校数学 基礎）の②を使います。

これをうまく使うと（√〇＋√△）（√〇ー√△）＝〇ー△　となり、

きれいにルートが外れます！

では、具体的なやり方を例題とともに見ていきましょう。

 赤文字は解答記述に普通現れない部分です。

ですが、赤文字の部分が最も重要です。

赤文字は考え方の部分（だから普通書かない）、

黒文字はその考え方にのっとった計算の部分です。

まず(1)です。

分母に√5 をかけてやれば分母のルートが外れます。

でもただ分母に √5 をかけるだけだとをかけることと同じなので

値が変わってしまいます。

ではどうしましょう？

１をかけても値は変わりません。

ならば、（これって１ですよね？）をかければ

値も変わらず分母からルートが外れませんか？

というわけで(1)の解答のようになります。

これ以外はただの平方根の計算なので練習して慣れましょう。

では(2)。

ここでは分母の 3-√7 が消えてほしいので、展開公式を利用して分母が消えるように、(1)と同じようにしてをかけます。

あとは計算していくと見事分母からルートがなくなります。

最後に(3)。

分母の項が３つ。

これがうまく消える展開公式は知らないですよね。

僕もぱっと思いつきません。

ではどうするか。

ここでも例の展開公式を使いましょう。

「でも項３つあるので使えません」ですって？

まあ、そう固いことを言わずに。

2+√3 と √5 に分けて例の公式を使います。

そうすれば、解答の２回目の赤文字達の直前の式になります。

でもまだ分母にルートがある。

だったら、もう一度有理化しましょう！！

そうして計算をしていくと見事最後は分母に根号がなくなります。

どうですか？

最後の問題なんか面倒ですが、

一気にやろうとすると分からなくなります。

一つ一つ、できる形に無理やりもっていって

何段階にも分けて有理化しましょう。

今回はここまで。

それではまた次回お会いしましょう。さようなら。