１次不等式と連立不等式【数Ⅰ】

１次不等式の解法

一言でいいます。

１次方程式と同じです。（※ただし不等号の向きに注意！！）

まあ、練習問題を通してみていきましょう。

［訂正］「不等号」の「号」の字を間違えてしまいました...すみません。

１次不等式と同じように左辺に文字を含んだ項を、右辺に定数項を移項します（もちろん左辺と右辺は逆でもＯＫ）。

そして１次不等式と同じように、左辺がxだけになるように式変形して終了です。

連立不等式

２以上の不等式が連立された連立不等式は、数直線を駆使します。

これは一例ですが、数直線では不等式をこのように表すことが多いです。

では、実際に問題をやってみましょう。

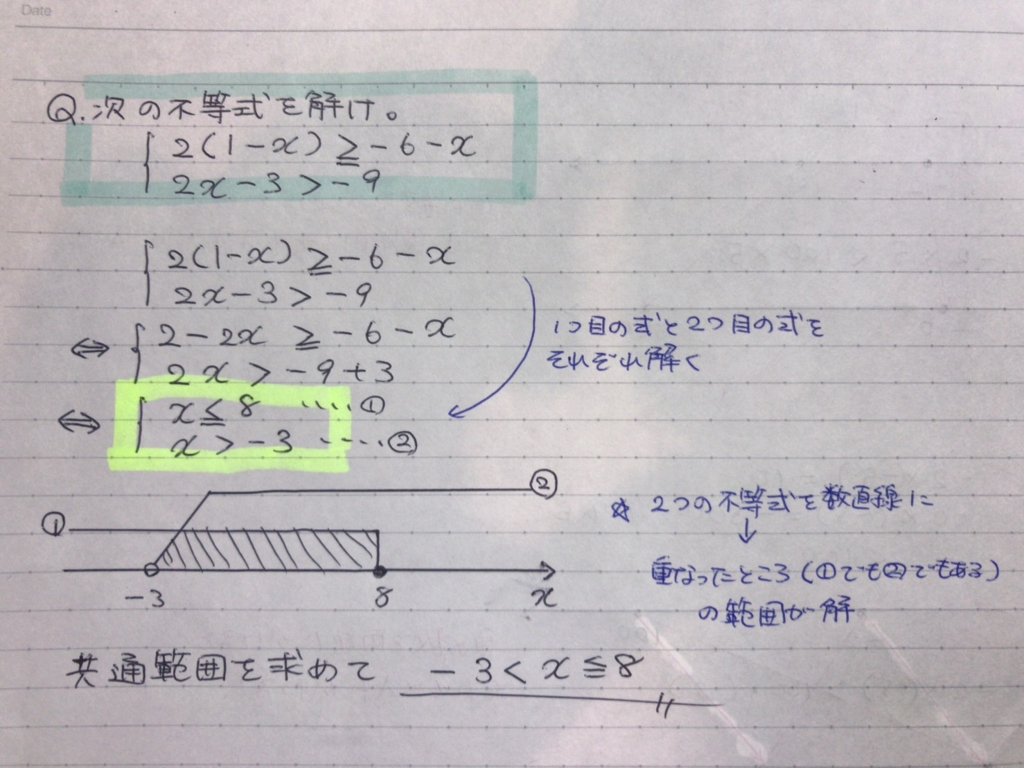
これは２本の１次不等式を連立させた連立不等式です。

まず、この２本の不等式をそれぞれ解きます。

そうすると、黄色の四角の中のようになります。

ここで気を付けるのが｛ は「～かつ・・・」という意味だということです。（後で集合の範囲で詳しくやります）

「～かつ・・・」なので、①でもあり②でもあるｘの範囲がこの連立不等式の解です。

①でもあり②でもある範囲は、２つの不等式を数直線にかいたときに重なる部分（範囲）です。ちなみに重なる部分がないとき、「解なし」といいます。（解がない、という答えです。「解」と「答え」は違うんですねえ）

もう１問。

前回のブログの言葉を借りますね。

この問題は自分で「和訳」してみましょう。

この問題のポイントは「分けて考える」ことです。

今回はここまで。

それではまた次回お会いしましょう。さようなら。