関数【数Ⅰ】
関数
定数:値が固定されて変化しない数のこと。ただしその値が具体的な数値として特定されていなくてもよい(つまり文字でもOK)。
変数:値が変化する数のこと。未知または定まっていない数を表す。
2つの変数x, yがあり、
xの値を決める→yの値がただ1つに定まる
とき、yはxの関数であるといいます。
また、yがxの関数であることを y=f (x)やy=g(x), y=h(x)のように表します。
これが超超超超超重要なのでかみ砕きます。
関数はよく自動販売機に例えられます。
自動販売機はボタンを押すとただ1つ決まった商品が出てきます。
関数y=f (x) も、
xの値を決める(ボタンを押す)とただ1つyの値が決まり(決まった商品が出てき)ます。
例えば
y=x+2
において、
x = 5 と決めると、ただ1つyの値は y = 7 に決まります。
なのでこの式においてyはxの関数です。
また、y = 3 と決めると、ただ1つxの値は x = 1 に定まるので
xはyの関数でもあります。→逆関数の存在(数Ⅲ)
y=x2
において、yはxの関数です。
ですが、y= 4 と決めてもxの値は x = ±2となり、ただ1つに決まりません。
なのでxはyの関数ではありません。
したがって、
yがxの関数であってもxはyの関数であるとは限らない
ということになります。
数学的な細かい考え方や数Ⅲで効いてくるのでぜひ知っておいてください。
値
関数 y=f(x) において、x=a のときのyの値を f(a) と書き、f(a) を f(x) の x=a における値といいます。
定義域・値域
以下、関数 y=f(x) を考えます。
定義域:xの値が取りうる範囲(xの変域)のこと。ex) y=√x の定義域は x≧0
値域:xが定義域全体を動くときのyの変域のこと。
定義域は(a≦x≦b)のように表すことが多いです。
また定義域について特に断りがないとき、xの定義域は実数全体であることが多いです。
座標
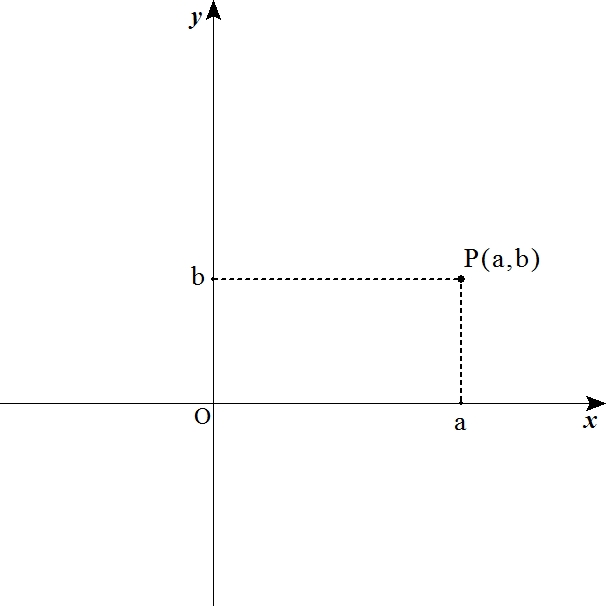
図のように平面上に座標軸(x軸・y軸)を定めると、その平面上のどんな点Pも図のような実数aとbの組で表されます。
この組(a, b)を点Pの座標といい、座標が(a, b)である点PをP(a, b) と表します。
座標軸が定められた平面を座標平面といいます。
また、座標平面で
・x>0かつy>0の領域を第1象限
・x<0かつy>0の領域を第2象限
・x<0かつy<0の領域を第3象限
・x>0かつy<0の領域を第4象限
といいます。
ただし、x軸とy軸はどの象限にも含まれません。
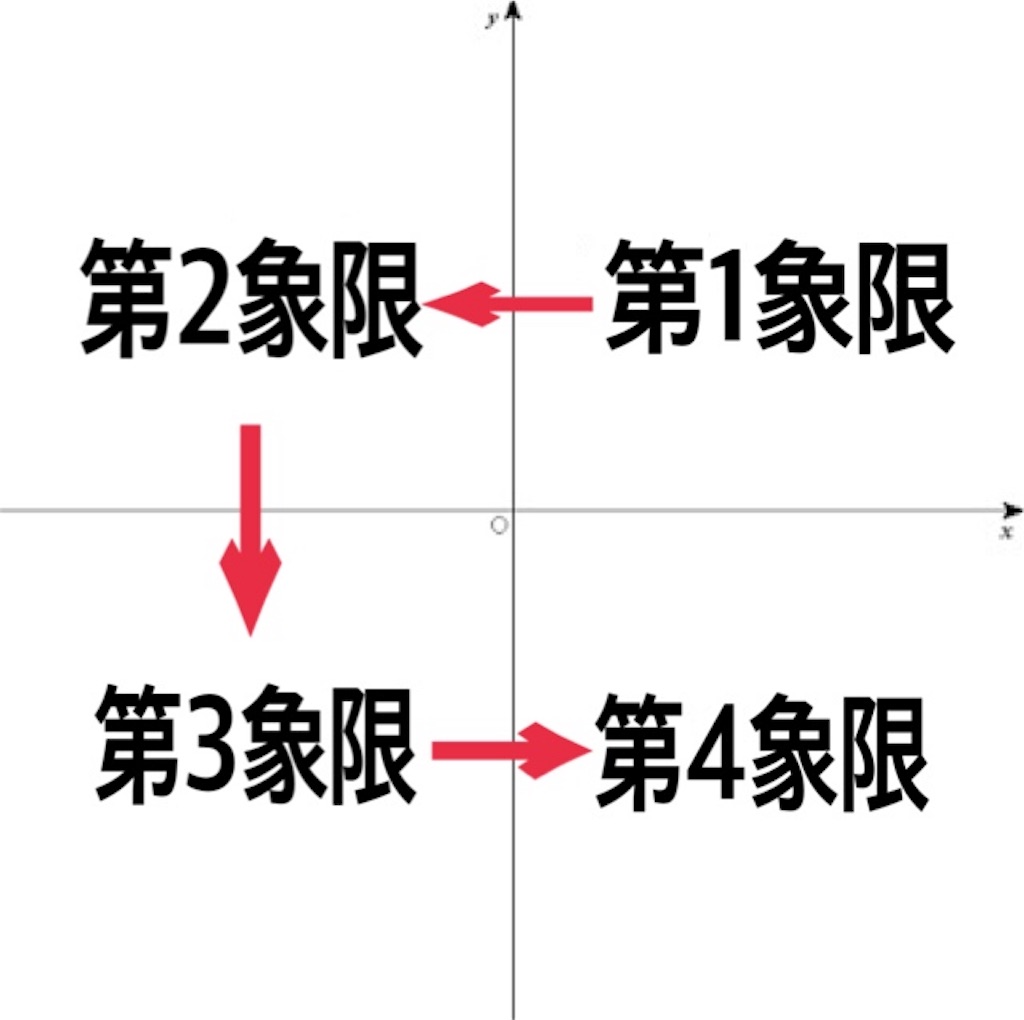
右上から反時計回りですね♪